Medidas de Dispersão

Medida de dispersão é uma forma de medir o quanto um dado foge da média. Esse assunto é muito importante para o ENEM, porém normalmente é cobrado por meio de lógica e não por contas.

Amplitude total

É a medida mais simples de todas, basta subtrair o maior dado do menor dado.

Desvio médio

É como se fosse uma amplitude total, mas subtrai-se o dado (xi) da média (M) e divide-se pelo numero de dados (n). É como uma combinação de amplitude total com media aritmética simples, veja:

$DM = \frac{\sum | x_{i} - M |}{\sum n}$

Variância

Variância é a média dos quadrados dos desvios médios, ou seja, é a mesma fórmula dos desvios médios mas ao quadrado. Então pode ser escrita assim:

$Δ = \frac{\sum {(x_{i} - M)}^{2}}{n}$

Normalmente, não utilizamos a resposta da questão como a variância, pois ela apresenta uma unidade de medida ao quadrado, por exemplo, se os dados estiverem em metros, a variância estará em metros quadrados. Para resolver isso, tiramos a raiz quadrada da variância, obtendo o desvio padrão.

Desvio Padrão

É simplesmente a raiz quadrada da variância.

$DP = \sqrt{Δ}$

Agora a unidade de medida não está mais ao quadrado, o que significa que podemos utilizá-la para comparar os desvios dos dados.

Coeficiente de Variação

O coeficiente de variação surge como uma forma de transformar o desvio padrão em uma porcentagem, para que possamos comparar os desvios de dados que possuem unidades de medida diferentes. Podemos calcular o coeficiente de variação dividindo o desvio padrão pela média, assim:

$CV = \frac{DP}{M} \times 100$

Exercícios de Exemplo

Questão 1

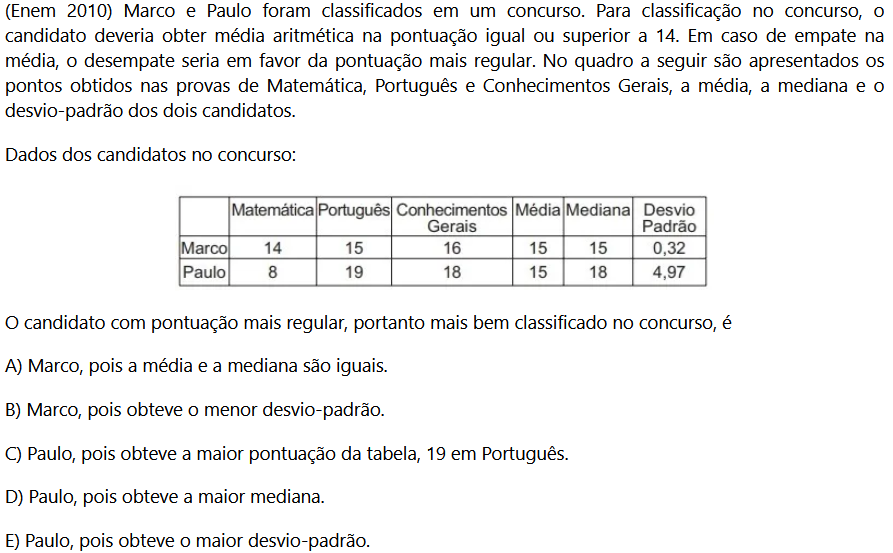
Fonte: https://exercicios.mundoeducacao.uol.com.br/exercicios-matematica/exercicios-sobre-desvio-padrao.htm#questao-10053

Nesta questão basta analizarmos os dados fornecidos pela tabela e pelo enunciado. O critério de desempate é o quão homogêneo as notas foram, logo a mediana não é um critério de desempate, por isso podemos eliminar a alternativas A e D. Similar a isso, a nota em portugues não é um critério de desempate, então podemos eliminar a alternativa C. Sobraram as alternativas B e E, analisando os dados, vemos que a nota mais homogênea é a de Marcos, pois ela é quase 0. Logo a alternativa correta é a letra B.

Questão 2

Fonte: https://exercicios.mundoeducacao.uol.com.br/exercicios-matematica/exercicios-sobre-desvio-padrao.htm#questao-10053

Se a variância X é 0,81, logo o desvio-padrão de X é a raiz quadrada de 0,81. Logo, √0,81 = 0,9
Parecido com isso a variância Y é 0,64 e o desvio padrão será √0,64, que é 0,8.
Com essas informações, podemos eliminar as alternativas A, D e E. Na alternativa C, temos: 0,9 - 0,8, pois a alternativa fala da diferença do desvio padrão e não da variancia, caso fosse a diferença da variância, aí sim essa alternativa estaria correta.
Nesse caso, só nos falta a alternativa B, que é a correta.

Questão 3

Calcule: desvio médio, variância, desvio padrão e coeficiente de variação dos dados apresentados na tabela.

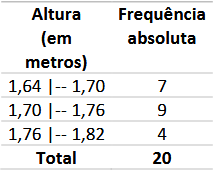
Fonte: Adaptado do material da professora Valéria Espindola Lessa.

Classes médias:

$\frac{1.64 + 1.70}{2} = 1.67 \frac{1.70 + 1.76}{2} = 1.73 \frac{1.76 + 1.82}{2} = 1.79$

Calculo da Média:

$M = \frac{\sum f_{i} \cdot x_{i}}{\sum f_{i}} = \frac{7 \cdot 1.67 + 9 \cdot 1.73 + 4 \cdot 1.79}{20} = \frac{34.42}{20} = 1.721$

Desvio médio aplicando a fórmula:

$DM = \frac{\sum | x_{i} - M |}{n} = \frac{0.732}{20} = 0.0366$

Variância:

$Δ = \frac{7 \cdot {(1.67 - 1.721)}^{2} + 9 \cdot {(1.73 - 1.721)}^{2} + 4 \cdot {(1.79 - 1.721)}^{2}}{20} = 0.00214$

Desvio Padrão:

$DP = \sqrt{0.00214} = 0.0463$

Coeficiente de Variação:

$CV = \frac{0.0463}{1.721} \times 100 % = 2.69 %$

>>Proximo Conteúdo
>>Página de Conteúdos