Portfólio de Matemática

O que são?

Matrizes são um tipo de tabela utilizada na matemática para organizar números. Elas são escritas assim:

$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$$

Forma Geral

Toda matriz é composta por linhas e colunas, assim como tabelas. Os elementos da primeira linha começam em a11, a12, a13, e assim por diante. A segunda linha começa em a21, a22, a23, e assim por diante. Podemos escrever assim também:

$$A_{m\times n}=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ ⋮& ⋮& \dots & ⋮\\ a_{m1}& a_{m2}& \dots & a_{mn}\end{array}\right]$$

Matriz Diagonal

São os elementos na diagonal da matriz (tanto da direita para esquerda, quando da esquerda pra direita).

$$A=\left[\begin{array}{cccc}\ddots & \mathrm{x}& x& \mathrm{\ddots }\\ \mathrm{x}& \ddots & \ddots & \mathrm{x}\\ x& \ddots & \ddots & x\\ \mathrm{\ddots }& \mathrm{x}& x& \ddots \end{array}\right]$$

⋱ São os elementos da diagonal.

Matriz Triangular

Possui zeros nas pontas

$$U=\left[\begin{array}{cccc}{u}_{11}& u_{12}& \dots & u_{1n}\\ 0& u_{22}& \dots & u_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & u_{nn}\end{array}\right]$$

Soma e Subtração de Matrizes

Só pode ser feita em matrizes de mesma ordem (mesmo "tamanho").

Para somarmos ou subtrairmos duas matrizes basta somar ou subtrair os elementos correspondentes, como no exemplo:

$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]+\left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right]=\left[\begin{array}{cc}{a}_{11}+b_{11}& a_{12}+b_{12}\\ a_{21}+b_{21}& a_{22}+b_{22}\end{array}\right]$$

↓

$$\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]+\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right]=\left[\begin{array}{cc}6& 8\\ 10& 12\end{array}\right]$$

Multiplicação por número escalar

Para multiplicarmos uma matriz por um número escalar, basta multiplicarmos cada elemento da matriz pelo número escalar. Veja o exemplo abaixo:

$$2\cdot \left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]=\left[\begin{array}{cc}2& 4\\ 6& 8\end{array}\right]$$

Multiplicação de Matrizes

Só pode ser feita se o numero de colunas do A for igual ao numero de linhas do B.

Para multiplicarmos 2 matrizes, devemos multiplicar cada elemento da linha da primeira matriz pelo elemento da coluna da segunda matriz e somar os resultados. Assim:

$$A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]B=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]C=A\cdot B=\left[\begin{array}{cc}{a}_{11}\cdot 1+a_{12}\cdot 3& a_{11}\cdot 2+a_{12}\cdot 4\\ a_{21}\cdot 1+a_{22}\cdot 3& a_{21}\cdot 2+a_{22}\cdot 4\end{array}\right]$$

↓

$$A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]B=\left[\begin{array}{cc}5& 6\\ 7& 8\end{array}\right]C=A\cdot B=\left[\begin{array}{cc}1\cdot 5+2\cdot 7& 1\cdot 6+2\cdot 8\\ 3\cdot 5+4\cdot 7& 3\cdot 6+4\cdot 8\end{array}\right]C=\left[\begin{array}{cc}19& 22\\ 43& 50\end{array}\right]$$

Transposição de Matrizes

Uma matriz transposta é uma matriz "ao contrario", suas linhas viram colunas e suas colunas viram linhas.

$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]A^T=\left[\begin{array}{cc}1& 4\\ 2& 5\\ 3& 6\end{array}\right]$$

Transformações Gráficas

Com matizes podemos simular figuras. Usamos a primeira linha como ponto X de um plano cartesiano e a segunda linha como ponto Y.

Translação

Muda o objeto de lugar. Por exemplo: um triângulo possui pontos (0, 2)(4, 2)(3, 6). Se mudarmos ele para (2, 2)(6, 2)(5, 6), ele se deslocou 2 unidades para a direita. Assim temos:

$$\mathrm{Posição}=\left[\begin{array}{ccc}0& 4& 3\\ 2& 2& 6\end{array}\right]+\left[\begin{array}{ccc}2& 2& 2\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}2& 6& 5\\ 2& 2& 6\end{array}\right]$$

Reflexão

Espelhamento da figura no eixo X ou Y. Para isso multiplicamos por:

$$\text{Reflexão no eixo X:} \left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\text{Reflexão no eixo Y:} \left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$$

Rotação

Rotação do ângulo θ da figura. Para isso multiplicamos por:

$$\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$$

Escala

Alterar a escala da figura. Para isso multiplicamos por:

$$\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]$$

Sendo Sx a largura da figura e Sy a altura da figura.

Exercícios Exemplos

Questão 1

(ENEM 2023 - PPL) Os candidatos A, B e C participaram de um concurso composto por uma prova de Matemática, uma de Português e outra de Geografia, sendo os pesos dessas três provas diferentes. As notas obtidas por esses três candidatos e os pesos atribuídos a essas provas estão representados nas tabelas:

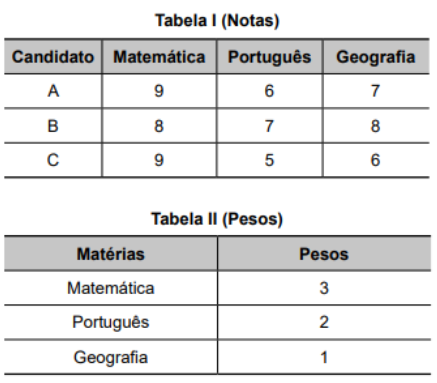
As notas finais são obtidas somando-se os produtos das notas pelos respectivos pesos. As notas finais dos três candidatos podem ser obtidas multiplicando-se a matriz das notas dos três candidatos nas três provas pela matriz dos pesos das três provas. A matriz das notas finais dos três candidatos é:

Aqui devemos calcular a nota final de cada candidato, usando um dos dois métodos que a questão nos deu, eu preferi multiplicar a nota pelo peso. Assim:

Candidato A:

$9\times 3+7\times 1+6\times 2=27+7+12=46$

Candidado B:

$8\times 3+8\times 1+7\times 2=24+8+14=46$

Candidato C:

$$ 8\times 3+5\times 1+7\times 2=24+5+14=43$$

Logo a matriz das notas finais é:

$$\left[\begin{array}{c}46\\ 46\\ 43\end{array}\right]$$

Questão 2

(ENEM 2021)Uma empresa avaliou os cinco aparelhos de celulares (T1, T2, T3, T4 e T5) mais vendidos no último ano, nos itens: câmera, custo-benefí cio, design, desempenho da bateria e tela, representados por I1, I2, I3, I4 e I5, respectivamente. A empresa atribuiu notas de 0 a 10 para cada item avaliado e organizou essas notas em uma matriz A, em que cada elemento aij significa a nota dada pela empresa ao aparelho Ti no item Ij. A empresa considera que o melhor aparelho de celular é aquele que obtém a maior soma das notas obtidas nos cinco itens avaliados.

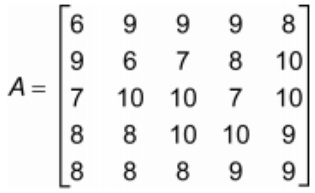
Com base nessas informações, o aparelho de celular que a empresa avaliou como sendo o melhor é?

Essa questão nem precisa de cálculo, podemos apenas analisar o seguinte: as linhas são os Ts e as colunas são os Is. Logo, a linha que tiver maior soma das notas é o aparelho melhor. Olhando por cima percebemos que a linha 4 possui 2 notas iguais a 10, 2 notas iguais a 8 e uma nota igual a 9. Logo, por apresentar a maiores números, a linha 4 é a melhor.