Portfólio de Matemática

O que é?

A estatística é um ramo da matemática que estuda a coleta, organização, análise e interpretação de dados. No ensino médio estudamos a estatística descritiva, que é a parte da estatística que estuda como resumir a pesquisa com tabelas e gráficos. Também existe a estatística inferencial, que só é estudada no ensino superior.

Termos da estatística

• População: é o conjunto de todos os elementos que estão sob análise.
• 
  Amostra: parte da população.
• 
  Pesquisa Qualitativa: é uma pesquisa com foco em qualidade, preferências do analisado. Normalmente é dado em forma de texto.
• 
  Pesquisa Quantitativa: é uma pesquisa com foco em quantidade, normalmente é dado em forma de números.
• 
  Frequência Absoluta: é o número de vezes que um valor aparece em uma pesquisa.
• 
  Frequência Relativa: é a frequência absoluta dividido pelo número de elementos da amostra.
• 
  Frequência de Classes: número de vezes que um intervalo de valores aparece num conjunto de dados. É dado por um intervalo aberto-fechado, ou seja, se tivermos 3|-5 nossa classe começa em 3 e termina em 4,9.

Média Aritmética Simples

É a média básica que aprendemos no fundamental, é dada pela soma dos elementos, dividido pela quantidade de elementos. Na formula: xi = dado, n = quantidade de dados.
$$\frac{\sum _{i=1}^n{x}_i}{n}$$

Média Ponderada

Similar a média aritmética simples, porém apresenta pesos. Nessa média multiplicamos o dado pelo peso e dividimos pela soma dos pesos. $$\frac{\sum _{i=1}^n{x}_i{p}_i}{\sum _{i=1}^n{p}_i}$$

Moda e Mediana

• Moda: Termo que mais aparece em uma sequencia de dados.
• 
  Mediana: Termo do meio de uma sequencia de dados. Na mediana é obrigado a organizar os dados em ordem crescente ou decrescente. Se o numero de dados for ímpar a mediana é o termo "do meio". Se o numero de dados é par, temos que fazer a média dos dois dados do meio.

Exercício Exemplo

Calcule a média ponderada, mediana e moda dos dados fornecidos abaixo:

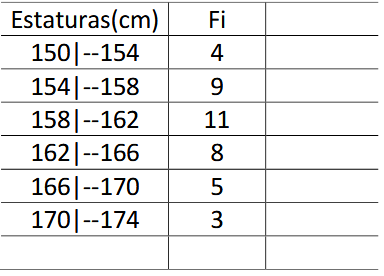
Fonte: Adaptado do material da professora Valéria Espindola Lessa.

Para a média ponderada temos que multiplicar cada dado pelo seu peso e dividir pela soma dos pesos: $$\begin{array}{lll}\mathrm{x\_1}=\frac{150+154}{2}=152& \mathrm{f\_1}=4& \mathrm{x\_1}\times \mathrm{f\_1}=152\times 4=608\\ \mathrm{x\_2}=\frac{154+158}{2}=156& \mathrm{f\_2}=9& \mathrm{x\_2}\times \mathrm{f\_2}=156\times 9=1404\\ \mathrm{x\_3}=\frac{158+162}{2}=160& \mathrm{f\_3}=11& \mathrm{x\_3}\times \mathrm{f\_3}=160\times 11=1760\\ \mathrm{x\_4}=\frac{162+166}{2}=164& \mathrm{f\_4}=8& \mathrm{x\_4}\times \mathrm{f\_4}=164\times 8=1312\\ \mathrm{x\_5}=\frac{166+170}{2}=168& \mathrm{f\_5}=5& \mathrm{x\_5}\times \mathrm{f\_5}=168\times 5=840\\ \mathrm{x\_6}=\frac{170+174}{2}=172& \mathrm{f\_6}=3& \mathrm{x\_6}\times \mathrm{f\_6}=172\times 3=516\end{array}$$ $$\frac{\sum _{i=1}^n{x}_i{p}_i}{\sum _{i=1}^n{p}_i}$$

↓

$$\frac{6440}{40}=161$$

Logo, temos que a média ponderada é 161cm. Para a mediana, temos que encontrar o numero do meio. A sequencia já está em ordem crescente, então não precisamos organizar. Temos como total de elementos a soma dos fi:

$$n=40$$

Como metade do total temos:

$$\frac{n}{2}=\frac{40}{2}=20$$

Como a frequencia que apresenta o 20º elemento é 158-162, temos que a mediana é 160cm.

Agora para a moda temos: A frequência que mais se repete é a 158|-162, logo nossa moda está ali. Fazendo a média entre 158 e 162 novamente temos que nossa moda é igual a mediana, 160.